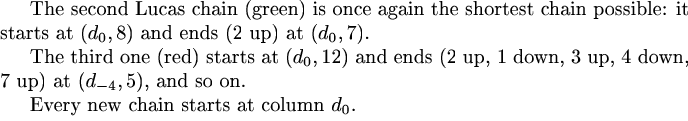The Bergman number system

In 1957 George Bergman published his number system that operates analogous to the binary system, only based on the power of phi. The expansion of a base phi number is not unique: two succesive 1’s can be replaced by a 1 in the column prior to both and the reverse is possible too (100=011). This is called the golden mean flip. Because this way a 1 at the end of the expansion endlessly can be replaced by 011 the truncation rule has been introduced that says that 011 at the end of the expansion is not allowed.

When in an expansion the number of 1’s are minimalized, which means that two succesive 1’s are not allowed, and the truncation rule is applied, this expansion is called the Bergman expansion. Starting with the addition 1+1=2 and adding 1 over and over again, when the golden mean flip will be appied when necessary, all the Bergman expansions can be found. It has no identifiable structure.

When the rule that two succesive 1’s are not allowed will be restricted with the exception that in the column 0 and 1 two 1’s at the same time are accepted when this occurs, this new representation, which has been called the canonical expansion, will have a structure based on the Lucas sequence.

This structure might be labelled as two-dimensional and amounts to the observation that the lenghts of the vertical runs of 1’s spread out in chains of consecutive Lucas numbers. They are called Lucas chains.