In general

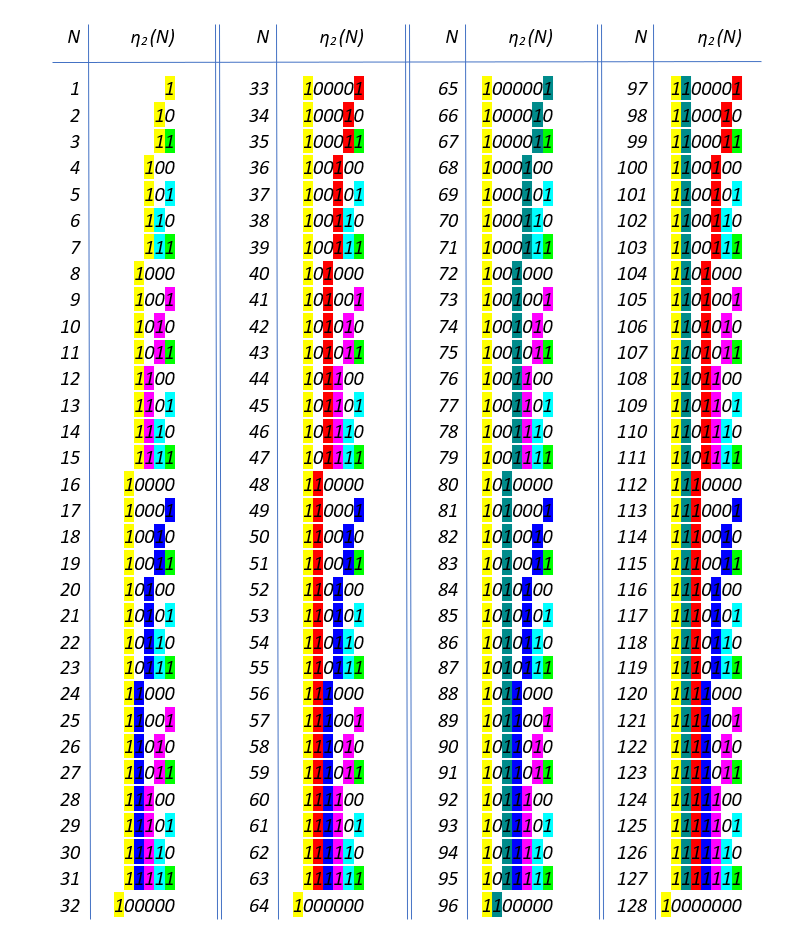
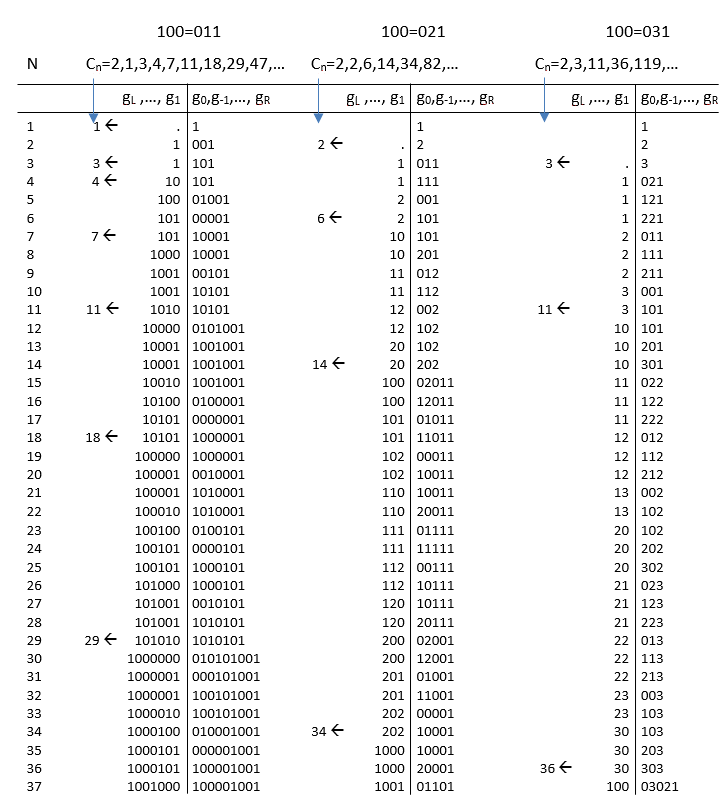
The general definition of the base 100=0pq number systems will lead to the general 100=0pq flip. When 100=011, as we have seen, the structure of the number system is fully based on Lucas chains. When p increases the structure of companion chains can still be recognized. When q also increases the stucture of companion chains will become less visible, although the companion sequence remains the basic structure.

Some highlights of this general number system will be mentioned and illustrated with examples:

• When 0<q<p there won’t be any problem to built a valid number system.
• When 0<p<q  it won’t be possible to built a valid number system using the 100=0pq flip. But there are exceptions, for instance the base q number systems of which the base 2 number system (binary numbers) and the base 10 number system (natural numbers) the best known are.
• A negative p leads to a mirrored number system when q=1. When q>1 the mirror structure won’t no longer be there.
• A negative q leads to the base 10q=0p0 number systems with q=|q| and under certain conditions to the complex mean.
• A negative p and q will lead to an impossibe flip, what won’t mean that it is impossible to built a number system.