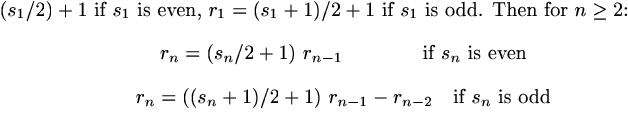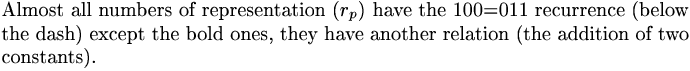Counting representations
Abstract
The expansions of base 100=011 number system are not unique. Using the 100=011-flip it is possible to transform the expansion with a minimal number of 1’s to an expansion with a maximal number of 1’s. During this proces all representations of the expansion can be found. The method of counting the number of possible representations will be explained.
The structure of the Bergman expansion will be discussed. It seems there is a certain mirror symmetry and most of the numbers of representations have a Fibonacci based structure.
The Zeckendorf number system also has such a mirror symmetry, but the Fibonacci based structure has a parewise relation that is not based on Fibonacci.
The Bergman number system is a special case (p=1) of the base 100=0p1 number system. The method of counting representations therefore will been transformed into a general form. As an example the base 100=021 number system is looked at. It has a mirror symmetry and a kind of doubling. The structure is based on the Pell numbers and is partly Fibonacci related (the relation between the odd numbers and the even numbers are different).
- 1 The method of counting
- 2 The Bergman expansion
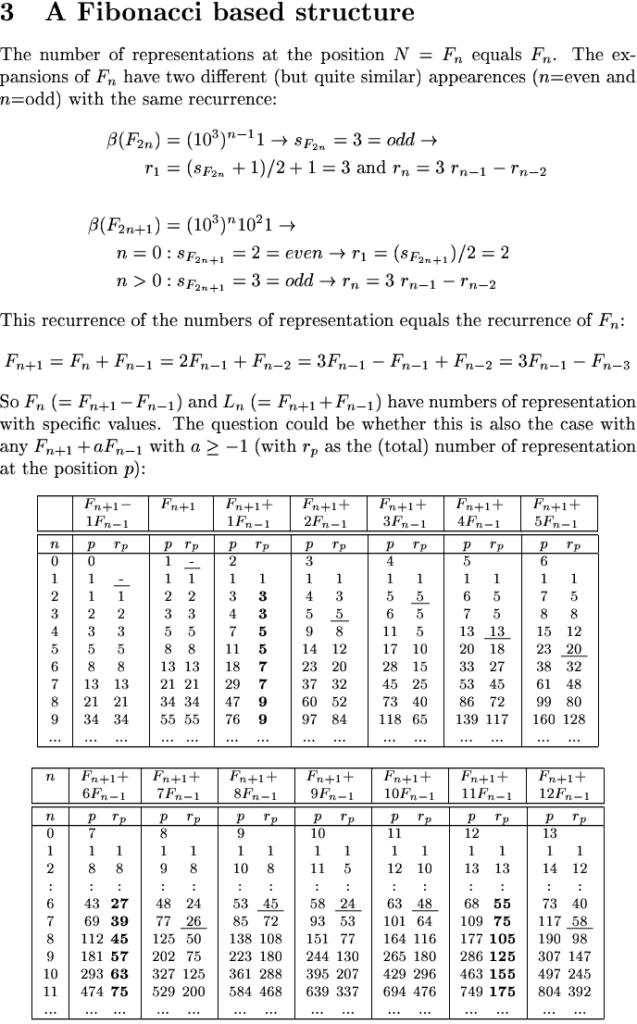
- 3 A Fibonacci based structure
- 4 The Zeckendorf number system
- 5 The base 100=0p1 number systems
- 6 The base 100=021 number system